Light Guiding Light

(Let light be the master of its own destiny)

by Allan W Snyder and François Ladouceur

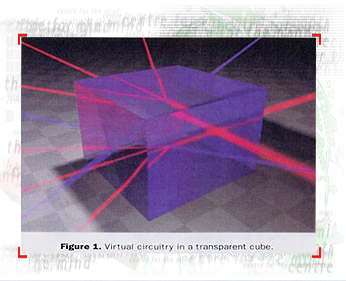
The present on-going revolution in photonics could see its summit with the ultimate all-optical device. Simply imagine a transparent cube like that of Fig. 1 with a myriad of interconnections and components created by light alone. This is our dream. Circuits that lie on top of one another and are reconfigurable. Virtual circuitry. No physical "wires". Either light itself directs and manipulates light without any intervening fabricated components such as optical waveguides, or light is used to write ideal optical components and circuitry in photosensitive materials. Light controls its own destiny.

The story of guiding light with light and of creating virtual circuitry is not just about an emerging technology and the ingenious efforts on the part of many who are presently attempting to make it a reality. Research into this field has also revealed new conceptual and experimental approaches for understanding how curious light beams, known as optical spatial solitons, can be made to remain localized in space while performing some rather amazing acrobatics. Advances of late have been remarkably swift, coming from different groups across the globe: Spatial solitons, once the domain of high power lasers, can now be launched by an incandescent light bulb. Soliton dynamics, once the province of esoteric mathematics, is now accessible with undergraduate physics. Mere theoretical predictions of a few years ago, such as the possibility of one soliton being made to spiral about another, the fusion or the creation of solitons upon collision, and the transportation of a dim beam by a bright beam are now readily observable in the laboratory. Even popular science magazines have questioned whether fabricated optical components would eventually become obsolete for device applications.

This article conveys the conceptual aspects of light guiding light by using the simplest known models. It also speculates on future applications once all the bugs are ironed out, although we are here limited only by our imagination.

Solitons from a Linear Perspective

As we said, the building blocks for light guiding light are free-standing beams, known as spatial solitons. Unlike linear waves which diffract, solitons create their own channel as they travel in a uniform nonlinear medium, remaining localized and preserving their shape. Beams in a linear medium do not influence each other. But solitons can attract, repel, spiral around each other and this interaction can even be described by the classical force laws treating the beams as particles with mass. Whereas linear waves always pass through one another, solitons can be dramatically altered by collisions. They can annihilate one another, fuse (Fig. 2) or give birth to multiple solitons. These phenomena turn out to be of potential importance to the emerging technology of light guiding light and light written circuitry. Clearly, we need to have a physical understanding of solitons.

To set the stage, we recall the physics of optical waveguides. Optical beams have an innate tendency to spread as they propagate in a homogeneous medium. However, this beam diffraction can be compensated for by the lens like action of beam refraction, if the refractive index is increased in the region of the beam. The resulting optical waveguide provides a balance between diffraction and refraction.

Spatial solitons can also be understood from this familiar perspective. Conceptually speaking, nonlinear beams interact with matter to create their own waveguides. This occurs because the refractive index of a nonlinear medium depends on the physical properties of the light beam. We emphasize that these induced waveguides are composed of linear material and are of arbitrary shape, even twisted and contorted. Beams then propagate along their own induced waveguide according to the familiar physics of linear optics. Of course, if you change the initial conditions, then you change the form of the induced waveguide.

From this elementary perspective, we can appreciate that disparate types of solitons are actually the same animal. In the simplest case, a soliton is one mode of the waveguide it induces. This describes the classical optical soliton of Chaio, Garmire and Townes as well as the more esoteric solitons such as the so-called vortex solitons. More generally, a soliton can be two or more modes of the induced waveguide. This elaboration explains interesting soliton dynamics, incoherent solitons, multi-humped solitons and the coexistence of different classes of solitons.

Now, if a soliton can be composed of a number of modes, each travelling at a different speed, then it should be possible to decompose the soliton into its constituent modes in exact analogy to Newton's refraction of white light by a prism into its component colours. And this elementary physics foreshadows novelties such as symmetric soliton beams being transformed into asymmetric beams upon colliding with one another.

The fact that nonlinear propagation has a linear waveguide equivalent provides a powerful conceptual tool, one that guides us in a physical manner to the fundamental equations and to their solutions. It allows us to predict novel phenomena, motivate light written circuitry, and foreshadow the design of lossless waveguide components as we discuss below. Put simply, all soliton dynamics have a linear waveguide analogue, albeit some unusual shaped waveguide system. Vice versa, every linear waveguiding phenomenon has its soliton equivalent in some nonlinear medium. A self-consistency relation unites the linear and nonlinear equivalents.

A Simple Model of Soliton Dynamics

One major challenge is to find a simple analytical description of solitons and their interactions. To achieve this, we need only borrow from the literature of the linear harmonic oscillator.

Because every linear optical waveguide has a soliton equivalent, it is natural to first consider the simplest optical waveguide possible, one whose refractive index falls off parabolically. Light beams obey the linear harmonic oscillator in this medium. This reveals that Gaussian beams remain Gaussian shaped as they propagate. In general the beams undulate periodically, undergoing periodic trajectories.

Now, according to the above linear perspective, Gaussian shaped solitons must also exist in some homogeneous nonlinear medium with the same behaviour as beams in a parabolic index optical waveguide. The particular nonlinear medium is found by using the self-consistency relation. Several candidates exist. But the simplest medium is one whose nonlinear induced refractive index change depends on the beam total power only. This arises, for example, when the medium has a nonlocal response with a correlation length that is much larger than the beam diameter. In such a medium, Gaussian shaped soliton beams remain Gaussian and they are unaltered by colliding with one another.

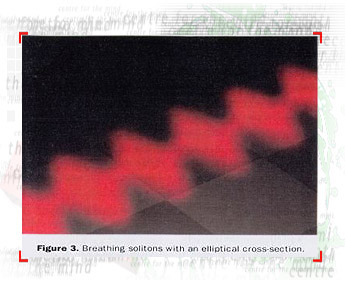
For a special beam radius and power, a Gaussian beam will propagate without change. Such a beam is called a stationary soliton. It induces a graded index optical fiber which can guide a signal beam. All other beams "breathe" as they propagate with their radius oscillating periodically (Fig. 3).

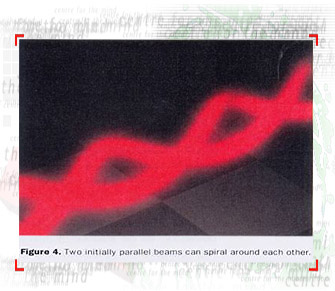
What happens to two stationary solitons that are initially launched in parallel to each other? In a homogeneous linear medium they would diffract as they travel in a straight trajectory. In this nonlinear medium they can attract and undergo periodic collisions with one another or, if launched skew to each other, spiral about each other as shown in Fig. 4. Finally, a distant "dim" beam can remain localized and be guided and steered by a "bright" soliton beam.

Solitons as Bundles of Classical Particles

Most experiments to date have involved comparatively narrow solitons launched by a coherent source. At the other extreme it is possible to have comparatively large incoherent solitons. And, in a beautiful experiment, Mitchell and Segev have launched them from an ordinary incandescent light bulb!

Such "big" incoherent solitons can be very neatly viewed as being composed of an enormous number of modes of the multimoded waveguide they induce. But, recall that diffuse light propagation along multimoded waveguides can be described by classical geometric optics. So incoherent solitons can also be viewed as bundles of rays, each ray obeying the paraxial ray equation, or equivalently as a bundle of classical (non-interacting) point particles, each particle obeying Newton's laws of motion.

This leads to predictions that are unique to incoherent solitons. For example, they can have any shape in their two-dimensional cross-section, even travel in parallel without interacting, unlike coherent beams in the same intensity dependent medium.

Temporal Solitons for Telecommunications

It is insightful to contrast spatial with temporal optical solitons. Temporal solitons are pulses that propagate along optical glass fibers[ ]for long distance telecommunications. Here the material nonlinearity is only weakly perturbed. This is a one-dimensional problem. Whereas, spatial solitons envisaged for device applications in bulk material are typically quasi-monochromatic beams that are localized in two-transverse dimensions and propagate only for millimeters. These beams sufficiently alter the refractive index of the bulk material to actually create their own waveguides. The extra dimension brings additional riches such as the possibility for beams to spiral around each other, but it also demands that the nonlinearity be saturating or nonlocalized if the beams are to be both stable and localized in space.

Device and Logic Applications: Switching Light with Light

The dream of photonics is to have a completely optical technology. Here the traditional carriers of information, electrons, are envisaged to be replaced by photons for devices based on switching and logic. Spatial solitons offer one potential way to achieve this dream. We have described how waveguides are induced by solitons. The challenge is to develop methods for controllable steering of these waveguides by light itself and to produce reconfigurable waveguides.

Because solitons can attract and guide beams, light can be used to switch light for various device and logic applications which are presently being performed by electronics. The solitons can be considered as the information flow itself or as inducing optical waveguides in which the information is carried. This information can take the form of a weak ("dim") probe beam at a different wavelength or different polarisation than the ("bright") soliton beam. In either scheme, intricate virtual circuitry can be written in bulk nonlinear media. Depending on the material, the circuitry has a life span which allows for the possibility of self-reconfigurable circuits. Such plasticity opens the door to adaptive circuits that can be designed to transform themselves to the desired application. We are led to the image of a transparent cube with thousands of dynamically interconnected "wires" all created, maintained and organised by light itself.

The speed required for switching depends on the application. It can be as slow as seconds for circuit reconfiguration in network application or as fast as picoseconds for optical computing. The steering of one soliton by another or of a weak signal beam by a soliton forms the simplest case of spatial switching. Alternatively, the coupling ratio of a soliton induced coupler can be adjusted by changing the pump signal in one arm. Structures can be created to tap a signal, make a copy or reroute it and these processes can be made dynamic. It is also possible for two colliding solitons to fuse or for a soliton to be split into two solitons by a weak probe beam, thus creating additional forms of spatial switching.

Designer components and light written circuitry

We have shown how soliton dynamics can be approached from the perspective of linear waveguides. Curiously the reverse is also true. The phenomenon of soliton dynamics provides a method of actually fabricating waveguide components whose design had not even been foreshadowed from our knowledge of linear waveguides. The concept is elementary. Solitons are allowed to interact in the appropriate photosensitive material so that the desired induced waveguide configurations are then permanently written.

For example, consider the optical device known as the X-junction. This is one of many building block components used for processing optical signals. It can be used to mix or split two signals in any desired proportion. Figure 5 shows a signal propagating through a soliton induced X-junction. In this particular case, the junction is designed to be completely transparent.

Light written circuitry offers potential advantages over the more conventional fabrication processes such as ion diffusion, PECVD, and sol-gel. In some materials beams fuse upon colliding. But, unless beams collide at virtual grazing incidence, they always pass through one another without influencing each other. In this way it is possible to compress circuitry into a compact space with many circuits sharing the same physical location. Furthermore, certain photosensitive materials offer the potential for erasing one light written device and replacing it by another. Hence, we have the building blocks for dense reconfigurable virtual circuitry.

Conclusions

We have unfolded our dream of virtual circuitry. A transparent cube with a myriad of interconnections created, maintained, and arranged by light itself - with truly awesome potential. Will all this lead to a viable technology? Some formidable challenges remain in crafting the requisite materials, but the present situation regarding light guiding light is reminiscent of the mid 1960's when optical fibre communication was first being mooted. A great idea, if glass absorption could be dramatically reduced. That reduction came in only a few years. Where there is a will, there is a way!

Scientists have been trying to confine light to artificial boundaries. Here is the opportunity for light to be the master of its own destiny.

Acknowledgements: Nail Akhmediev, Alexander Buryak, Barry Luther-Davies, Yuri Kivshar, Wieslaw Krowlikowski and John Mitchell contributed to the discussions presented here. Drew Whitehead and Tim Thompson produced the scientific visualizations.

References

1. R.Y. Chiao, E. Garmire, and C.H. Townes, "Self-trapping of optical beams", Phys. Rev. Lett. 13, 479-480 (1964)

2. Recent reviews include: M. Segev and G. Stegeman, "Self trapping of optical beams", Physics Today 51, 42-48 (1998); B. Luther-Davies, J. Christou, V. Tikhonenko and Yu. S. Kivshar, "Optical vortex solitons, JOSA B 14, 3045-3053 (1997); A.W. Snyder and Yu. S. Kivshar, "Bright spatial solitons in non-Kerr material", JOSA B 14, 3025-3031 (1997).

3. M. Mitchell and M. Segev, "Self-trapping of incoherent white light", Nature (London) 387, 880-882 (1997)

4. Y.R. Shen, "Solitons made simple", Science 276, 1520 (1997); A.W. Snyder and D.J. Mitchell, "Accessible solitons", Science 276, 1538-1541 (1997)

5. A.W. Snyder, D.J. Mitchell, and F. Ladouceur, "Self-induced optical fibers: spatial solitary waves," Opt. Lett. 10, 21-23 (1991)

6. L. Poladian, A.W. Snyder, and D.J. Mitchell, "Spiralling spatial solitions," Opt. Commun. 85, 59-62 (1991)

7. A.W. Snyder and A.P. Sheppard, "Collisons, steering and guidance with spatial solitons," Opt. Lett. 18, 482-484 (1993)

8. W.E. Torruellas, Z. Wang, D.J. Hagan, E.W. Van Stryland, G.I. Stegeman, L. Torner, and C.R. Menyuk, "Observation of two-dimensional spatial solitary waves in a quadratic medium," Phys. Rev. Lett. 74, 5036-5039 (1995)

9. M. Shih, M. Segev, and G. Salamo, "Circular waveguides induced by two-dimensional bright steady-state photorefractive screening solitons," Opt. Lett. 21, 931-933 (1996)

10. M. Shih and M. Segev, "Incoherent collision between two-dimensional bright steady-state photorefractive spatial screening solitons," Opt. Lett. 21, 1538-1540 (1996)

11. V. Tikhonenko, J. Christou, and B. Luther-Davies, "Three-dimensional bright spatial soliton collision and fusion in a saturable nonlinear medium," Phys. Rev. Lett. 76, 2698-2701 (1996)

12. W. Krolikowski and S.A. Holmstrom, "Fusion and birth of spatial solitons upon collision," Opt. Lett. 22, 369-371 (1997)

13. M. Shih, M. Segev, and G. Salamo, "Three-dimensional spiralling of interacting spatial spatial solitons," Phys. Rev. Lett. 78, 2551-2554 (1997)

14. T. Thwaites, "Will optical fibres become obsolete?" New Scientist, January 12, p. 14 (1991)

15. D.J. Mitchell, A.W. Snyder, and L. Poladian, "Interacting self-guided beams viewed as particles: Lorentz force derivation", Phys. Rev. Lett. 77, 271-273 (1996)

16. A.W. Snyder, S. Hewlett, and D.J. Mitchell, "Dynamic spatial solitons," Phys. Rev. Lett. 72, 1012-1016 (1994); A.W. Snyder, D.J. Mitchell, and Yu. S. Kivshar, "Unification of linear and nonlinear guided wave optics," Mod. Phys. Lett. B 9, 1479-1506 (1995)

17. A.W. Snyder, L. Poladian, and D.J. Mitchell, "Stable black self-guided beams of circular symmetry in a bulk Kerr medium," Opt. Lett. 17, 789-791 (1992)

18. G.A. Swartzlander, Jr. and C.T. Law, "Optical vortex solitons observed in Kerr nonlinear material," Phys. Rev Lett. 69, 2503-2506 (1992)

19. N.N. Akhmediev, W. Krolikowski, and A.W. Snyder, "Partially coherent solitons of variable shape," Phys. Rev. Lett. in press (November 1998)

20. The concept of an incoherent soliton was first introduced in the temporal domain: A. Hasagawa, "Dynamics of an ensemble of plane waves in nonlinear dispersive media," Phys. Fluids 18, 77 (1975); Envelope soliton of random phase waves, Phys. Fluids 20, 2155-2156 (1977); Self-confinement of multimode optical pulse in a glass fiber, Opt. Lett. 5, 416-417 (1980). Segev's group was first to recognize the possibility in space..

21. M. Mitchell and M. Segev, "Self-trapping of incoherent white light," Nature 387, 880-882 (1997).

22. D.N. Christodoulides, T.H. Coskun, M. Mitchell and M. Segev, "Multimode incoherent spatial solitons in logarithmically saturable nonlinear media," Phys. Rev. Lett. 80, 2310- 2313 (1998); M. Mitchell, M. Segev, T. Coskun and D.N. Christodoulides, "Theory of self-trapped spatially incoherent light beams," Phys. Rev. Lett. 79, 4990-4993 (1997)

23. A.W. Snyder, J.D. Love, Optical Waveguide Theory, Chapman and Hall (1983).

24. A.W. Snyder and D.J. Mitchell, "Big incoherent solitons," Phys. Rev. Lett. 80, 1422-1425 (1998)

25. A. Hasegawa, Optical Solitons in Fibers, Springer-Verlag, Berlin (1989).

26. F. Ladouceur, D.J. Mitchell, and A.W. Snyder, "Optical components induced by repelling solitons," JOSA B, 14, 1768-1771 (1997)

27. A.W. Snyder, A.V. Buryak, and D.J. Mitchell, "Beam splitting on weak illumination," Opt. Lett. 23, 4-7 (1998)

Allan W Snyder holds the Peter Karmel Chair of Science and the Mind at the Institute of Advanced Studies and is Head of the Optical Sciences Centre. François Ladouceur is a Research Fellow in the Optical Sciences Centre. Both are at the Research School of Physical Sciences and Engineering, the Institute of Advanced Studies, The Australian National University and both are part of the Australian Photonics Cooperative Research Centre.